Korrelaatiokertoimen määritelmän mukaan, jos kaksi muuttujaa on riippumattomia, niiden korrelaatio on nolla.Joten, ei voi tapahtua mitään korrelaatiota vahingossa!

$$ \ rho_ {X, Y} = \ frac {\ operaattorin nimi {E} [XY] - \ operaattorin nimi {E} [X] \ operaattorin nimi {E} [Y]} {\ sqrt {\ operaattorin nimi {E} [X ^ 2] - [\ operaattorin nimi {E} [X]] ^ 2} ~ \ sqrt {\ operaattorin nimi {E} [Y ^ 2] - [\ operaattorin nimi {E} [Y]] ^ 2}} $$

Jos $ X $ ja $ Y $ ovat riippumattomia, tarkoittaa $ \ operaattorin nimi {E} [XY] = \ operaattorin nimi {E} [X] \ operaattorin nimi {E} [Y] $ .Siksi $ \ rho_ {X, Y} $ osoittaja on tässä tapauksessa nolla.

Joten, jos et muuta korrelaation merkitystä, kuten täällä mainittiin, se ei ole mahdollista.Ellet selvitä määritelmääsi korrelaatiosta.

Comment näyte -korrelaatiosta. Verrattaessa kahta pientä riippumatonta otosta samankokoinen, näyte korrelaatio on usein huomattavasti erilainen kuin $ r = 0. $ [Mikään tässä ei ole ristiriidassa @ OmG: n vastauksen (+1) kanssa populaatio korrelaatiosta $ \ rho.] $

Harkitse korrelaatioita miljoonan itsenäisen parin välillä näytteet koosta $ n = 5 $ eksponentiaalijakaumasta nopeudella $ 1. $

  set.seed (616)
r = kopio (10 ^ 6, cor (rexp (5), rexp (5)))
keskiarvo (abs (r) > .5)
[1] 0,3886212
keskiarvo (r)
[1] -0.0005904455

hist (r, prob = T, br = 40, col = "taivaansininen2")
  viiva (v = c (-. 5, .5), col = "punainen", lwd = 2)
 

Tässä on esimerkiksi sirontakaavio miljoonasta näyteparista, joiden koko on $ 5, $ $ r = -0,5716. $

Eksponentiaalijakaumassa ei ole mitään erityistä tässä suhteessa. Vanhemman jakelun muuttaminen tavalliseksi yhtenäiseksi antoi seuraavat tulokset.

  set.seed (2019)
...
keskiarvo (abs (r) > .5)
[1] 0,391061
keskiarvo (r)
[1] 1.43269e-05
 

Sitä vastoin tässä on vastaava histogrammi yhtälöille paria normaalinäytteitä, joiden koko on $ n = 20. $

Huomaa: Muut tämän sivuston sivut käsittelevät $ r $ -jakelua tarkemmin; yksi heistä on tämä Q & A.

Yksinkertainen vastaus: jos 2 muuttujaa on riippumattomia, population-korrelaatio on nolla, kun taas sample-korrelaatio on tyypillisesti pieni, mutta ei nolla.

Tämä johtuu siitä, että otos ei edusta täydellisesti populaatiota.

Mitä suurempi otos, sitä paremmin se edustaa populaatiota, joten sitä pienempi korrelaatio sinulla on.infinite-näytteen korrelaatio olisi nolla.

Ehkä tästä on hyötyä joillekin ihmisille, joilla on sama intuitiivinen ymmärrys. Olemme kaikki nähneet jotain tällaista:

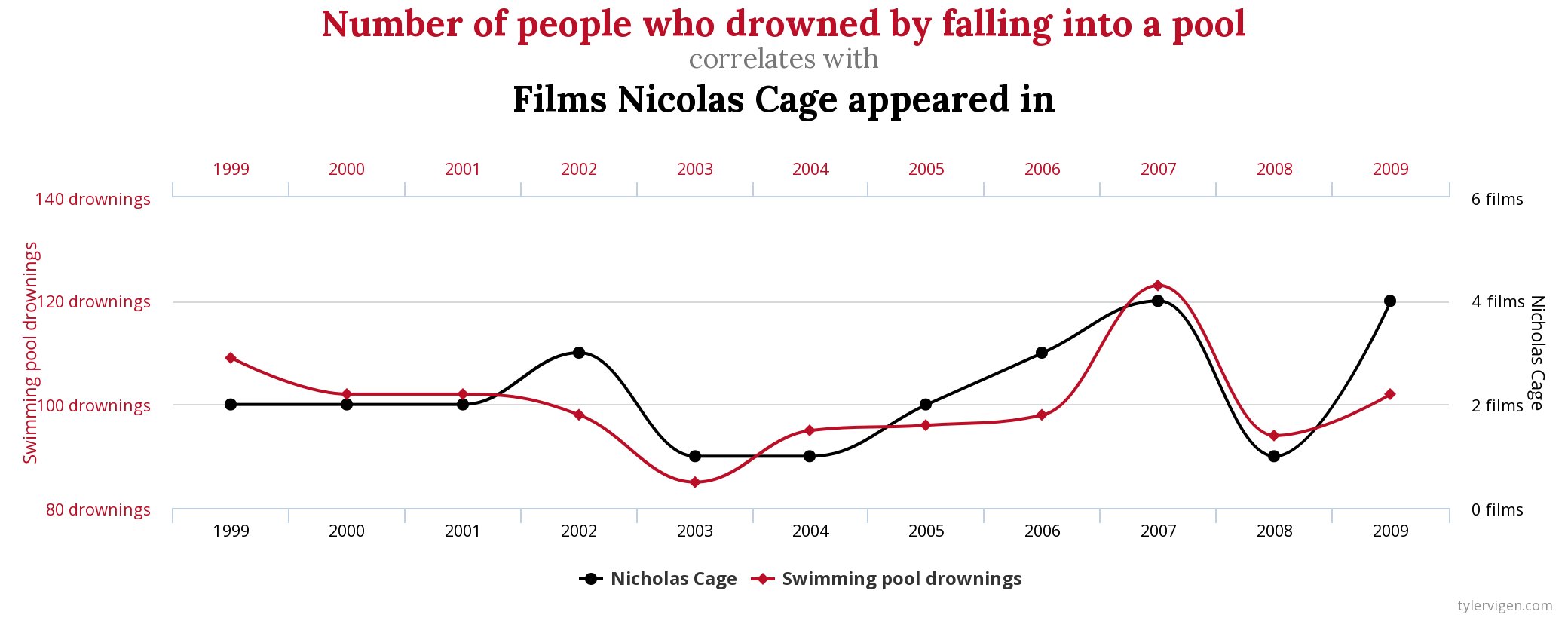
Nämä tiedot ovat oletettavasti riippumattomia, mutta niillä on selvästi korrelaatio ( $ r = 0,66 $ ). "Luulin, että riippumattomuus merkitsee nolla korrelaatiota!" opiskelija sanoo.

Kuten muut ovat jo huomauttaneet, sample-arvot korreloivat, mutta se ei tarkoita, että population: llä ei ole nolla-korrelaatiota.

Näiden kahden on tietysti oltava riippumattomia - kun otetaan huomioon, että Nicolas Cage esiintyi ennätyksellisessä 10 elokuvassa tänä vuonna, meidän ei pitäisi sulkea paikallista uima-allasta kesäksi turvallisuussyistä.

Mutta kun tarkistamme, kuinka monta ihmistä hukkuu tänä vuonna, on pieni mahdollisuus, että ennätykselliset 1000 ihmistä hukkuvat tänä vuonna.

Tällaisen korrelaation saaminen on epätodennäköistä. Ehkä yksi tuhannesta. Mutta se on mahdollista, vaikka nämä kaksi ovat itsenäisiä. Mutta tämä on vain yksi tapaus. Ajattele, että siellä on miljoonia mahdollisia mitattavia tapahtumia, ja voit nähdä mahdollisuuden, että kahden todennäköisyydet, jotka antavat korkean korrelaation, ovat melko korkeat (joten yllä olevien kaltaisten kaavioiden olemassaolo).

Toinen tapa tarkastella sitä on, että kahden itsenäisen tapahtuman takaaminen aina korreloimattomilla arvoilla on itsessään rajoittavaa. Kun otetaan huomioon kaksi itsenäistä noppaa ja ensimmäisen tulokset, toiselle noppalle on tietty (huomattava) tulosjoukko, joka antaa jonkin verran nollakorrelaatiota. Toisen noppan tulosten rajoittaminen nolla korrelaatioon ensimmäisen kanssa on selkeä riippumattomuuden rikkomus, koska ensimmäisten noppien heitot vaikuttavat nyt tulosten jakautumiseen.